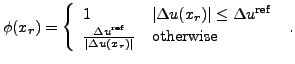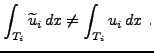Define the quantity 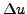 at a new set of (three)
collocation nodes
at a new set of (three)
collocation nodes 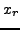 ,
, 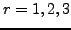 inside a mesh element
inside a mesh element 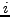 .
.
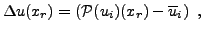 |
(25) |
where the projection
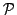 may be the projection onto the
space of linear function or the identity. If a cellwise neighborhood
has been used in step 1 the nodes
may be the projection onto the
space of linear function or the identity. If a cellwise neighborhood
has been used in step 1 the nodes 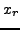 may be chosen at edge
midpoints, whereas for the nodal neighborhood the nodes of the
triangle are used.
may be chosen at edge
midpoints, whereas for the nodal neighborhood the nodes of the
triangle are used.
If one insists that the reconstructed solution must not exceed the
bounds established by the maximum and minimum volume averages of a
chosen local neighborhood, denoted by
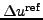 the
limiter will be activated whenever the
magnitude of
the
limiter will be activated whenever the
magnitude of 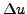 exceeds the magnitude of the allowed variation
exceeds the magnitude of the allowed variation
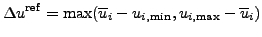 |
(26) |
at any of the nodes 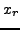 . The quantity
. The quantity 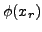 may be defined as
may be defined as
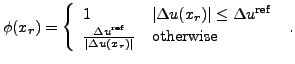 |
(27) |
Whenever 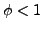 the local reconstruction may be modified according to
the local reconstruction may be modified according to
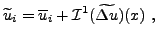 |
(28) |
where
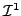 is the linear interpolation operator defined by
the nodes
is the linear interpolation operator defined by
the nodes 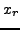 , and
, and
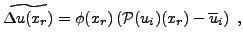 |
(29) |
A modification may be introduced by rejecting any
limiting whenever
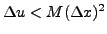 , where
, where 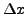 is
a characteristic mesh length. This will prevent a modification of the
solution near smooth extrema and is related to the theory of
total-variation boundedness (TVB) [3]. In
practice we usually choose values of
is
a characteristic mesh length. This will prevent a modification of the
solution near smooth extrema and is related to the theory of
total-variation boundedness (TVB) [3]. In
practice we usually choose values of 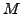 between 0 and 40.
between 0 and 40.
The procedure is sufficient to ensure that the reconstruction stays within the
prescribed bounds, but it is not conservative in the sense that in general
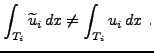 |
(30) |
A further modification of the linear solution is proposed
in [5] , which ensures conservation in a way that
prevents an increase of the slope. We adopt this strategy for the
present work, omitting the technical details for the sake of brevity,
and refer instead to [5]. Our general procedure
becomes identical to the one described in [5] if a
cell-wise neighborhood is used to compute the maximum allowed
slope. In the present work we use the nodal neighborhood, and the full
reconstruction is evaluated at the nodes of the triangles and compared
to the reference state.
Georg May
2006-02-23
![]() at a new set of (three)
collocation nodes
at a new set of (three)
collocation nodes ![]() ,
, ![]() inside a mesh element
inside a mesh element ![]() .
.
![]() the
limiter will be activated whenever the
magnitude of
the
limiter will be activated whenever the
magnitude of ![]() exceeds the magnitude of the allowed variation
exceeds the magnitude of the allowed variation