Some Theory...
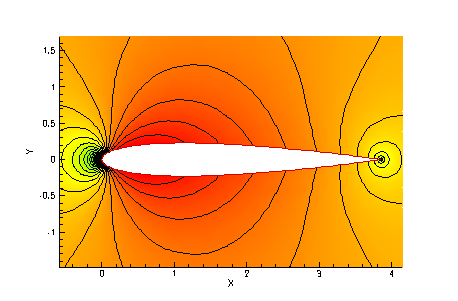
Figure 1 shows a solution of the Euler equations for
flow around the NACA0012 airfoil using the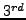 
order Spectral Difference scheme at flow conditions 
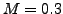and
zero angle of attack. Mach number
contours are shown on the left, while the figure on the right compares
the entropy error with results from a finite volume scheme, which
employs the CUSP scheme with a SLIP data reconstruction [7], and uses the
triangles as control volumes.
Figure 1:
Validation of the Spectral Difference Method: Subsonic flow
around the NACA0012 airfoil.
  |
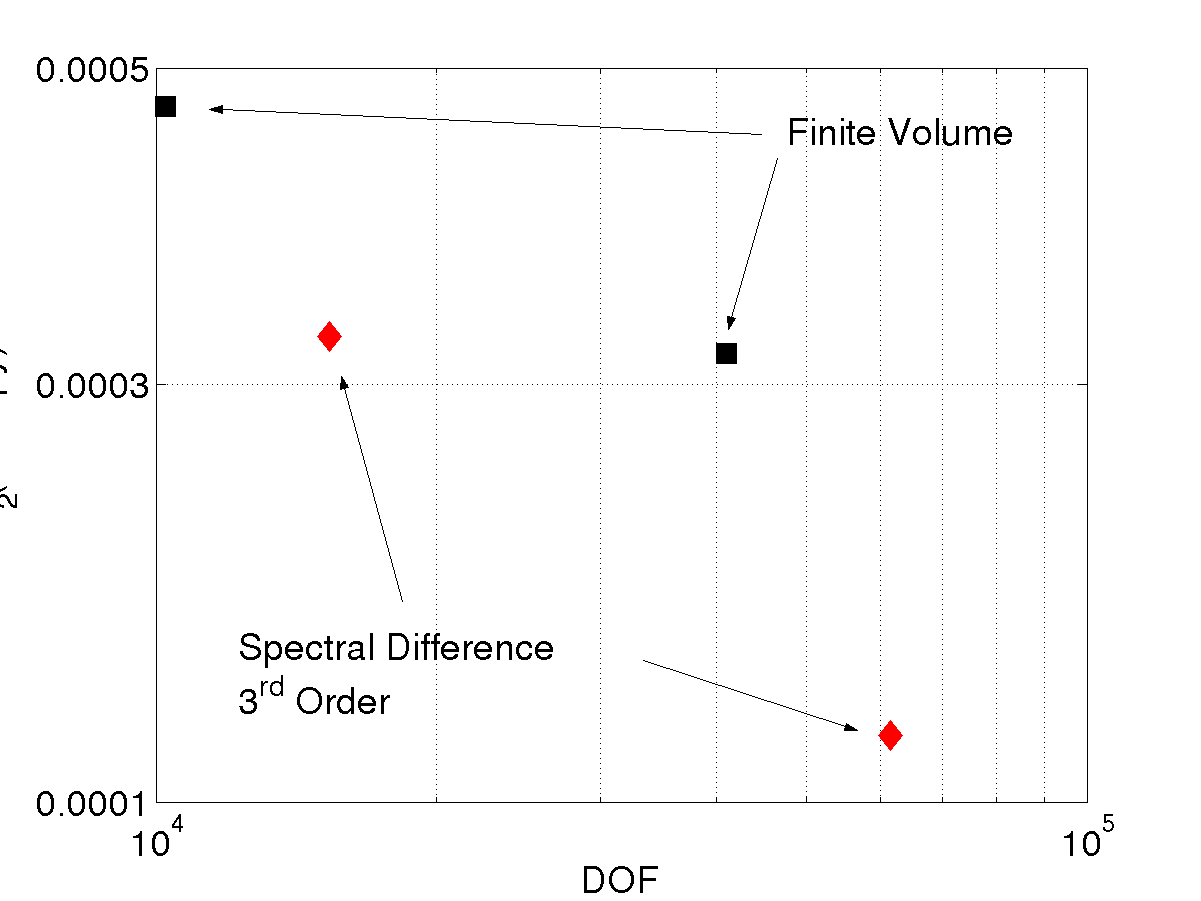Note that the entropy error for
the spectral difference scheme with 15,360 DOF is
roughly equal to the entropy error of the finite-volume scheme with
approximately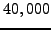 
DOF
Some Theory...
The famous mach reflection case...
The shocks are very well captured using a local-projection type
limiter, very similar to the one proposed for Discontinuous Galerkin methods.
A validation for low-Reynolds-number flow can be seen below
Figure 2:
Validation of the Spectral Difference Method: Subsonic viscous flow
around the NACA0012 airfoil. Left: Spectral Difference, 3rd
order. Right: Computational mesh
  |
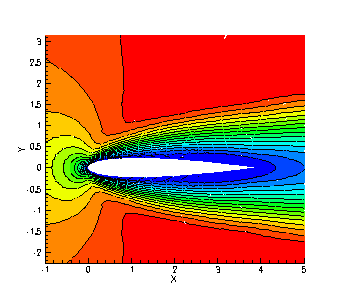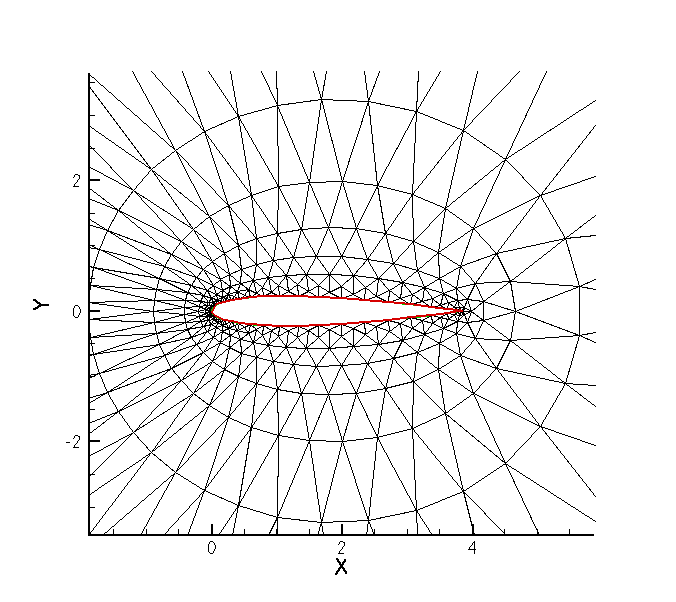The 3rd order SD scheme resolves the flow even on this coarse
mesh. This is not the case for a 2nd order finite volume scheme as is
shown below, which clearly demonstrates the superiority of the higher
order scheme.
Figure 2:
Subsonic viscous flow
around the NACA0012 airfoil. Finite Volume Schemes, 2nd
order. Right: Computational mesh
 |
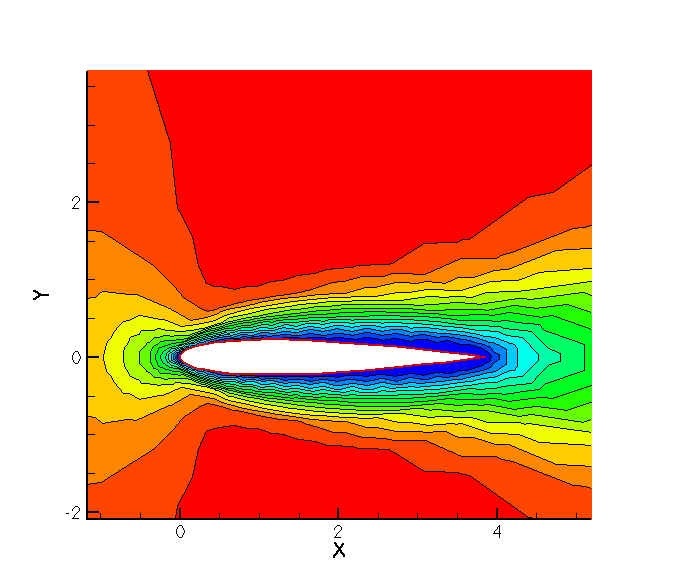Georg May
2006-02-23
