
Email: mcmu@stanford.edu
| Aerospace Computing Lab | Aero/Astro Department | Stanford University |
| Background |
| Education/Experience |
| Papers |
| Publications |
| Presentations |
| Posters |
| Research |
| NLFD Overview |
| NLFD-Cylinder |
| NLFD-Airfoil |
| NFLD vs Dual Time Stepping |
NLFD vs Dual Time Stepping Codes
A crucial question is whether the Non-Linear Frequency Domain method offers a major reduction in computational cost over established time-accurate methods. This chapter addresses this question by presenting a comparison of a state of the art time-accurate code UFLO82 [A. Jameson. Time Dependent Calculations Using Multigrid, with Applications to Unsteady Flows Past Airfoils and Wings. Technical Report 91-1596, AIAA 10th Computational Fluid Dynamics Conference, June 1991.N.A. Pierce and J.J. Alonso. Efficient Computation of Unsteady Viscous Flow by an Implicit Preconditioned Multigrid Method. AIAA Journal, 36:401 408, 1998.], with an NLFD code for Euler simulations of a pitching airfoil. In order to make a fair comparison the boundary conditions and spatial operators of the NLFD code have been replaced with exactly those of the UFLO82 code. With equivalent spatial errors the two codes can then be compared solely on their approximation of the temporal derivative in the conservation equations. A convergence study is first performed to quantify the error as a function of temporal resolution via time steps of modes. Using equivalent overall error levels the two codes are then compared on the basis of computational cost.
In the comparison of experimental and numerical results in the previous pages the flows contained only moderately strong shocks. In order to evaluate the NLFD method in the presence of strong nonlinear effects the case used in this section is more challenging. The reduced frequency and the dynamic angle of attack have been chosen to promote nonlinearites that result in a coupling of temporal modes within the flow field. The table below provides a list of the parameters defining this case.
| Airfoil | NACA 64A010 |
| Mean Angle of Attack | 0.0° |
| Angle of Attack Variation | ± 2.0° |
| Mach Number | 0.8 |
| Reduced Frequency | 0.05 |
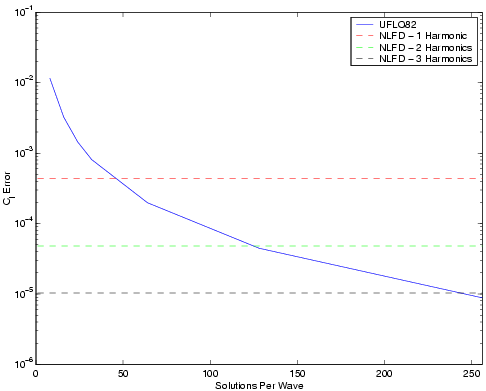
In order to quantify the required number of time steps per oscillation, a convergence study in temporal accuracy was performed for both codes running in unsteady mode. For UFLO82 the residual at the end of each time step was driven to machine zero. This code was run at 8 different temporal resolutions including 8, 16, 24, 32, 64, 128, 256 and 512 points per wavelength. To eliminate any error associated with initial transients, 48 periods of the airfoil oscillation were simulated. As the solution evolved in time, Fourier transforms of the latest period of coefficient of lift and moment were computed. The magnitude of the fundamental harmonic of these data sets is used to quantify the error. The control solution was selected from the last oscillation of the most accurate solution (512 points per wave), and is subtracted from all other solutions to quantify the error due to the temporal resolution
Similar runs were made with the NLFD code using one, two and three time varying modes. All components of the unsteady residual were driven to zero, and Fourier transforms of coefficient of lift and moment were computed from the periodic steady state solution. The magnitude of the fundamental harmonic was then subtracted from the control solution in a manner consistent with the UFLO82 results.
Each solution approaches an error level representing the minimum error achievable in realistic environments. These minimum errors are replotted on the figures below as a function of the temporal resolution used by each UFLO82 calculation. Overplotted on these figures are horizontal lines from NLFD calculations with varying numbers of temporal modes.
|
Error in Coefficient of Lift
|
Error in Coefficient of Moment
|
 |
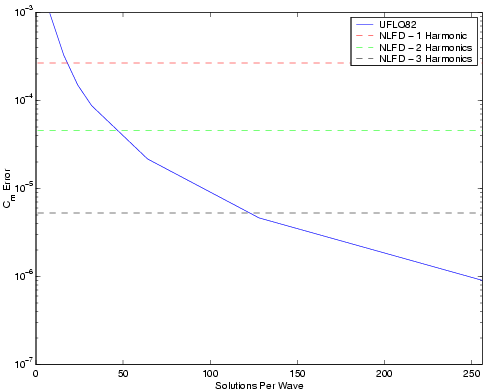 |
The intersection of the NLFD lines with the UFLO82 curve shows the temporal resolutions each code must use to achieve equivalent error levels. This data is summarized in the table below. Using coefficient of lift as a figure of merit, the NLFD code needs only 1 temporal mode to obtain similar error levels as a UFLO82 code using 45 points per wavelength. Using Cm in the same capacity, the UFLO82 code needs only 18 points for one mode in the NLFD code. Regardless of the figure of merit, for every additional temporal mode added in the NLFD calculation, the temporal resolution of UFLO82 needs to be increased by roughly a factor of 2.5 to 3.
| NLFD Modes | Coefficient of Lift UFLO82 Solutions Per Period | Coefficient of Moment UFLO82 Solutions Per Period |
| 1 | 45 | 18 |
| 2 | 125 | 45 |
| 3 | 244 | 123 |
The cost of the two solvers can now be compared using data presented in my dissertation. This comparison assumes that the work associated with a single multigrid cycle is equivalent between the two codes. This is an accurate approximation, given that UFLO82 and the NLFD code use the same pseudo-time advancement, residual averaging and multigrid aggregation and prolongation operators. This approach provides a relative comparison independent of the machine or compiler optimization algorithms. These latter parameters affect the cost of each method, but code implementation and profiling details are not the focus of this research.
The tables below provide the relative cost data using coefficient of lift and moment as the figures of merit. If the user requires equivalent error levels for both coefficients, then the lift results will drive the cost comparison. In this case, the NLFD code is a factor of 8 to 19 times faster than the UFLO82 code depending on the error level. In the worst case, using only moment error as the basis for comparison, the NLFD code at the lowest temporal resolution is approximately 3 times faster the UFLO82 code. Not surprisingly, the marginal cost of the NLFD solver is also better than the UFLO82 code. For either figure of merit, the cost multiple between the two codes increases in favor of the NLFD method as the number of modes is increased.
| Efficiency based on Coefficient of Lift | |||
| NLFD Modes | NLFD Cost(multigrid cycles) | UFLO82 SPP | UFLO82 Cost(multigrid cycles) |
| 1 | 135 | 45 | 1080 |
| 2 | 308 | 125 | 3750 |
| 3 | 526 | 244 | 10248 |
| Efficiency based on Coefficient of Moment | |||
| NLFD Modes | NLFD Cost(multigrid cycles) | UFLO82 SPP | UFLO82 Cost(multigrid cycles) |
| 1 | 113 | 18 | 324 |
| 2 | 257 | 45 | 1080 |
| 3 | 475 | 123 | 4428 |
Last Modified: March 20 18:08:00 PDT 2003